PROYECTO DE SINTESIS
LIBRO VIRTUAL DE MATEMATICASla matematica se creo ase 70.000 años atras de antigüedad, que están adornados con hendiduras en forma de patrónes geometricos También se descubrieron afectos preistoricos en afrca y francia, datados entre el35.000y 20.000el a.C., que sugieren intentos iniciales de el tiempo.Hay evidencias de que las mujeres inventaron una forma de llevar la cuenta de su de 28 a 30 marcas en un hueso o piedra, seguidas de una marca distintiva. Más aún, los cazadores y pastores empleaban los conceptos de uno, dos y muchos, así como la idea de ninguno o cero, cuando hablaban de manadas de animales.
el rey matematico
Erase una vez un rey que sabia mucho de las matematicas y quiso hacer una clase de matematicas y les enseño las fracciones propias
EJEMPLO:
BUENO AHORA UNA IMPROPIA
3
Bueno ahora la equibalente
5 10
Ahora les enseñare las fracciones en la recta
Ejemplo
6
ahora les voy a enseñar las fracciones de una cantidad
3 de20 - 15 porque 20 dividido 4 es 5 por3 es igual a 15
4 -
NÚMEROS MIXTO
Un numero mixto esta conformado por un numero entero y una fracción
5 3
4
CONVERSIÓN DE UN NUMERO MIXTO A UNA FRACCIÓN IMPROPIA
6 2 4 por el 6 más 2es igual a 26 pero el denominador queda igual
4 26
4
CONVERSIÓN DE FRACCIÓN IMPROPIA A NUMERO MIXTO
17 17divido 3 es igual a 2 al residuo y 5 al cociente
3 el residuo es el numerador el cociente es el numero 5 2
entero y el denominador es el mismo 3
FRACCIONES HOMOJENEAS
Las fracciones homojeneas tienen el mismo denominador
ejemplo
5 , 3, 9
6 6 6
SUMA Y RESTA DE FRACCIONES HOMOJENEAS
Para sumar o restar fracciones homojeneas se coloca el mismo denominador y los numeradores se suman o se restan.
EJEMPLO
suma: 5 + 3 +7 igual 15
12 12 12 12
RESTA: 22 - 7 IGUAL 15
40 40 40
SUMA Y RESTA DE FRACCIONES HETEROGÉNEAS
Las fracciones heterogeneas son las que tienen diferente denominador
Para sumar o restar fracciones heterogeneas se convierten a fraciones homogéneas ,para eso se halla el m.c.m por descompocicion de factores primos
4/5+7/12+3/6=48/60+35/60+30/60=113/60
descompocicion
5 12 6 2
5 6 3 2
5 3 3 3
5 1 1 5
1
MULTIPLICACIÓN DE FRACCIONES
Para multiplicar 2 o más fracciones, se multiplica numeradores con numeradores y denominadores por denominadores
Para dividir fracciones se multiplica el numerador por el denominador y el denominador por el numerador
EJEMPLO
8/5dividido3/4=32/15
3 PERIODO
havia una vez un niño muy tonto que no sabia sobres clases de rectas ni angulos ni otras cosas màs.
entonces lo mandaron a un colegio llamado james rodrigues y le enseñaron.
rectas secantes:son rectas que se cruzan en algún punto.
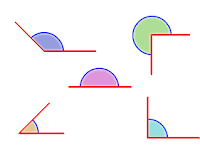
angulos
los angulos son un punto donde chocan 2 o mas rectas
o donde inician 2 semirectas o mas
angulo agudo:
mide - de90º
angulo recto:
mide 90º
angulo obtuso:
mide + de 90º pero- de 180º
angulo llano :
mide 180º
angulo concavo:mide mas de 180º
POLIGONOS:es una poligonal serrada .
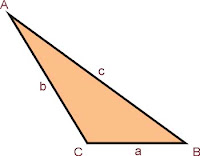
FIGURAS DE 3 LADOS
triangulo equilatero:
tiene sus tres lados iguales
TRIANGULO ISOCELES.
ahora les voy a enseñar las fracciones de una cantidad
3 de20 - 15 porque 20 dividido 4 es 5 por3 es igual a 15
4 -
Un numero mixto esta conformado por un numero entero y una fracción
5 3
4
CONVERSIÓN DE UN NUMERO MIXTO A UNA FRACCIÓN IMPROPIA
6 2 4 por el 6 más 2es igual a 26 pero el denominador queda igual
4 26
4
CONVERSIÓN DE FRACCIÓN IMPROPIA A NUMERO MIXTO
17 17divido 3 es igual a 2 al residuo y 5 al cociente
3 el residuo es el numerador el cociente es el numero 5 2
entero y el denominador es el mismo 3
FRACCIONES HOMOJENEAS
Las fracciones homojeneas tienen el mismo denominador
ejemplo
5 , 3, 9
6 6 6
SUMA Y RESTA DE FRACCIONES HOMOJENEAS
Para sumar o restar fracciones homojeneas se coloca el mismo denominador y los numeradores se suman o se restan.
EJEMPLO
suma: 5 + 3 +7 igual 15
12 12 12 12
RESTA: 22 - 7 IGUAL 15
40 40 40
SUMA Y RESTA DE FRACCIONES HETEROGÉNEAS
Las fracciones heterogeneas son las que tienen diferente denominador
Para sumar o restar fracciones heterogeneas se convierten a fraciones homogéneas ,para eso se halla el m.c.m por descompocicion de factores primos
4/5+7/12+3/6=48/60+35/60+30/60=113/60
descompocicion
5 12 6
5 6 3
5 3 3
5 1 1
1
MULTIPLICACIÓN DE FRACCIONES
Para multiplicar 2 o más fracciones, se multiplica numeradores con numeradores y denominadores por denominadores
EJEMPLO
2/4 * 3/5 * 1/2=6/40=3/20
DIVISIÓN DE FRACCIONESPara dividir fracciones se multiplica el numerador por el denominador y el denominador por el numerador
EJEMPLO
8/5dividido3/4=32/15
3 PERIODO
havia una vez un niño muy tonto que no sabia sobres clases de rectas ni angulos ni otras cosas màs.
entonces lo mandaron a un colegio llamado james rodrigues y le enseñaron.
CLASES DE RECTASRECTASLas rectas se nombran con letra mayuscula
RECTA:
Es una linea que no tiene comienzo ni fin
RECTA:
Es una linea que no tiene comienzo ni fin
rectas secantes:son rectas que se cruzan en algún punto.
angulos
los angulos son un punto donde chocan 2 o mas rectas
o donde inician 2 semirectas o mas
angulo agudo:
mide - de90º
angulo recto:
mide 90º
angulo obtuso:
mide + de 90º pero- de 180º
angulo llano :
mide 180º
angulo concavo:mide mas de 180º
POLIGONOS:es una poligonal serrada .
FIGURAS DE 3 LADOS
triangulo equilatero:
tiene sus tres lados iguales
TRIANGULO ISOCELES.
tiene dos lados iguales.
.
TRIANGULO ESCALENO:
tiene todos sus lados diferentes.
FIGURAS DE 4 LADOS
CUADRADO:Tiene todos sus lados iguales
RECTÁNGULO:Tiene dos lados iguales.
ROMBO:Es un cuadrado que descansa en una de sus vertices
ROMBOIDE O PARALELOGRAMO
TRAPECIO(isoceles):Tiene 2 lados iguales
TRAPECIO RECTO:Tiene un angulo recto
TRAPEZOIDE:Tiene todos sus lados diferentes.
FIGURAS DE MAS DE CINCO LADOS
PENTÁGONO:Tiene 5 lados
HEXÁGONO:Tiene6 lados
HEPTÁGONO:Tiene 7 lados
OCTÁGONO:Tiene 8 lados
NONÁGONO:Tiene 9 lados
DECAGONO:Tiene10 lados
PERÍMETRO
Es la suma de la longitud de los lados de una figura.Se simboliza con la letra P
EJ.
P=4cm+4cm+3cm+3cm
P=14cm
UNIDADES DE SUPERFICIE
se multiplica lado por lado
A=LXL
8cm
A=8cmX8cm
A=64cm2
se multiplicala base por la altura
A=BXA

rombo:
A = (D · d) / 2

trapecio:
A = (B + b) · h / 2

paralelogramo:
El paralelogramo es un polígono que tiene 4 lados, que son iguales y paralelos, de dos en dos.
Los ángulos son distintos de 90º. La suma de los 4 ángulos es de 360 grados.
El área se halla con la formula siguiente.
A = b · h

poligono regular:
En este apartado están los polígonos regulares que tienen más de 4 lados iguales. Los ángulos también son iguales.
El de 5 lados se llama pentágono. El de 6 lados hexágono, etc.
Para calcular el área de estos polígonos se utiliza la siguiente formula:
A = (P · a) / 2

MEDIDAS DE LONGITUD:
MEDIDAS DE volumen:
Rotación:

TRASLACIÓN:

semejansa:

congruencia:

circurferencia:
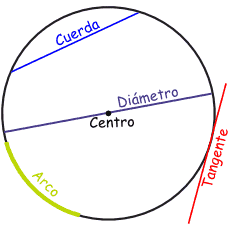
.
TRIANGULO ESCALENO:
tiene todos sus lados diferentes.
FIGURAS DE 4 LADOS
CUADRADO:Tiene todos sus lados iguales
RECTÁNGULO:Tiene dos lados iguales.
ROMBO:Es un cuadrado que descansa en una de sus vertices
ROMBOIDE O PARALELOGRAMO
TRAPECIO(isoceles):Tiene 2 lados iguales
TRAPECIO RECTO:Tiene un angulo recto
TRAPEZOIDE:Tiene todos sus lados diferentes.
FIGURAS DE MAS DE CINCO LADOS
PENTÁGONO:Tiene 5 lados
HEXÁGONO:Tiene6 lados
HEPTÁGONO:Tiene 7 lados
OCTÁGONO:Tiene 8 lados
NONÁGONO:Tiene 9 lados
DECAGONO:Tiene10 lados
PERÍMETRO
Es la suma de la longitud de los lados de una figura.Se simboliza con la letra P
EJ.
P=4cm+4cm+3cm+3cm
P=14cm
UNIDADES DE SUPERFICIE
Las unidades de superficie sirben para medir areas.La unidad principal es M2.
para realizar una combersion de una medeida grande a una pequeña se multiplica por 100 y cuando se hace una convercion de una unidad menor a una mayor se divide por 100
para realizar una combersion de una medeida grande a una pequeña se multiplica por 100 y cuando se hace una convercion de una unidad menor a una mayor se divide por 100
Km2 àX100àhm2 àX100àDam2àX100àM2àX100àdm2àX100àcm2àX100àmm2
______________________________________________________________________________________________
______________________________________________________________________________________________
Km2 ß/100ßhm2 ß/100ßDam2ß/100ßM2ß/100ßdm2ß/100ßcm2ß/100ßmm2
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
ÁREA AL CUADRADO__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
se multiplica lado por lado
A=LXL
8cm
A=8cmX8cm
A=64cm2
se multiplicala base por la altura
A=BXA
rombo:
A = (D · d) / 2
trapecio:
A = (B + b) · h / 2
paralelogramo:
El paralelogramo es un polígono que tiene 4 lados, que son iguales y paralelos, de dos en dos.
Los ángulos son distintos de 90º. La suma de los 4 ángulos es de 360 grados.
El área se halla con la formula siguiente.
A = b · h
poligono regular:
En este apartado están los polígonos regulares que tienen más de 4 lados iguales. Los ángulos también son iguales.
El de 5 lados se llama pentágono. El de 6 lados hexágono, etc.
Para calcular el área de estos polígonos se utiliza la siguiente formula:
A = (P · a) / 2
MEDIDAS DE LONGITUD:
Km àX10àhm àX10àDamàX10àMàX10àdmàX10àcmàX10àmm
______________________________________________________________________________________________
______________________________________________________________________________________________
Km ß/10ßhm ß/10ßDamß/10ßMß/10ßdmß/10ßcmß/10ßmm
MEDIDAS DE volumen:
Km3 àX1000àhm3àX1000àDam3àX1000àM3àX1000àdm3àX1000àcm3àX1000àmm3
______________________________________________________________________________________________
Km3 ß/1000ßhm3 ß/100ßDam3ß/1000ßM3ß/1000ßdm3ß/1000ßcm3ß/1000ßmm3
TRASLACIÓN:
semejansa:
congruencia:
circurferencia: